Solving Tic-Tac-Toe - Ear to the Bits

A few months ago, when I had decided that I wanted to quit my job as a C++ developer and become a web developer, I applied to the Flatiron School to immerse myself in web technologies. During the application process, I was assigned a code challenge, to create a game of Tic-Tac-Toe, played either by two humans or a human against an AI player, in the language of my choosing. To challenge myself, I chose Ruby, a language I had never used before but figured that there was never a better moment to start. I applied all of the object-oriented programming fundamentals I knew from my time coding in C++ and Java, and ended up with somethiing I was pretty proud of.

Refactoring

After the class was over, only four months after I wrote my first Ruby code, I went back to build upon what I had previously done. It’s fun to see how much better you’ve gotten at something, in my opinion. It was funny to see all of the non-Rubylike things I had done:

Accessing data elements outside of a class’s initialize method. For example, inside of my Board class:

def set(index, mark)
  @board[index] = mark
end

This I changed to

def set(index, mark)
  self.board[index] = mark
end

Using explicit return statements at the end of methods. I was used to the world of C++ in which best practice is to be as explicit as possible, otherwise your code is really difficult to read. Again, from the Board class:

def get(index)
  return @board[index]
end

I changed this method to

def get(index)
  self.board[index]
end

Unconventional method naming. What was with the question marks and exclamation points? I had written stuff like this (from Board class again):

def is_valid(index)
  if @board[index] == 'X' || @board[index] == 'O'
    return false
  else
   return true
  end
end

Also, what’s with those if and else statements? I was used to the C++ world in which that kind of logic ends up so verbose. I fixed it to look like this:

def valid?(index)
  return false if index < 0
  !self.board[index].nil? && self.board[index] != 'X' && self.board[index] != 'O'
end

Much more compact and readable, and better error checking!

Designing an AI

Once I had fixed my code to fit with Ruby conventions, I had a larger task to accomplish: make the AI unbeatable. I felt confident, as I had written an AI before for Battleship. However, it turns out that designing a Battleship strategy is different from Tic-Tac-Toe. A lot different, in fact, and it tripped me up.

When I designed the AI for Battleship, I created a board of probabilites, based on the likelihood of a ship being in a certain position on the board. I tried to do the same for Tic-Tac-Toe, even creating a ProbabilitiesBoard class that was initialized to look like this

      |     |
   3  |  2  |  3
 _ _ _|_ _ _|_ _ _
      |     |
   3  |  4  |  2
 _ _ _|_ _ _|_ _ _
      |     |
   3  |  2  |  3
      |     |

in which each number represents the number of different ways a player can win, based on the number of rows that interesect a position. Unfortunately, as I played out a few games and tried to recalculate my probabilities, I realised my calculation wasn’t robust enough. It didn’t take into account enough different possibilites of gameplay. Because, in Tic-Tac-Toe, unlike Battleship, you also have to block another player.

Tic-Tac-Toe is not like Battleship

So I was back to square one. I started to think about the game in certain types of moves. Certain moves won the game by making three in a row, certain moves blocked another player, certain moves created a dual threat, and so on. I had distilled the types of moves into a hierarchy as well, which looked something like this:

If you have two in a row, add a third to the row to win the game.
If your opponent has two in a row, add a third to the row to block him or her from winning.
Place your mark on the board strategically, bringing you closer to winning.

This was something. I quickly implemented two methods in the ComputerPlayer class, find_winning_move and find_blocking_move. Because I found that I need to iterate over all of the different rows in the board, I decided to store them in my Board class:

class Board
  attr_accessor :board
  attr_reader :rows

  def initialize
    @board = position_numbers
    @rows = [[0,1,2], [3,4,5], [6,7,8], [0,3,6],
             [1,4,7], [2,5,8], [0,4,8], [2,4,6]]
  end

  def position_numbers
    return *(1..9).collect { |x| x.to_s }
  end
  ...

Now, I could iterate though all of the rows and see if any of them had two ‘X’s or ‘O’s in a row:

def find_two_in_a_row(board, mark)
  board.rows.each do |row|
    if board.only_two_in_a_row?(row, mark)
      return board.get_open_position(row)
    end
  end
  nil
end

As you see, I created a separate method in the ComputerPlayer class called find_two_in_a_row, which iterates though all of the rows and tries to find two in a row of a mark passed in as a parameter. As soon as it finds a row, it returns with the empty position in the row.

A Hierarchical Strategy

I had created two crucial methods whith made the AI a lot smarter, but I was lost on the rest of the strategy. I decided to ask the Internet for some inspiration, and I found some help on Wikihow and Quora. However, I found it difficult to find patterns. I didn’t want to add a lot of if and else statements which check for things like “if the AI player went first and then the opponent moved in a corner” then “the AI player should put a mark in the opposite corner”. It didn’t feel right, and I felt like I could do better.

I had an aha moment when I came across this answer to a StackExchange question. It states that a Tic-Tac-Toe strategy is based on a hierarchy of types of moves. Of course! I had gotten halfway there when I realized that winning was more important than blocking which was more important that other types of moves, but I hadn’t been able to pin down the other types of moves. The hierarchy of moves is

The following algorithm will allow you (or the AI) to always deny your opponent victory:

Win: If you have two in a row, you can place a third to get three in a row.

Block: If the opponent has two in a row, you must play the third to block the opponent.

Fork: Create an opportunity where you have two threats to win (two non-blocked lines of 2).

Blocking an opponent’s fork: If there is a configuration where the opponent can fork, you must block that fork.

Center: You play the center if open.

Opposite corner: If the opponent is in the corner, you play the opposite corner.

Empty corner: You play in a corner square.

Empty side: You play in a middle square on any of the 4 sides.

Pick the highest possible on the list

I was able to knock out most of these methods pretty quickly, except for finding forks and blocking an opponent’s forks. These turned out to be trickier than I expected.

Finding Forks

In the case of finding a fork, I realized that a player only needed to find one in order to create a dual threat (and therefore win the game). I managed to map out an algorithm:

Iterate through all rows on the board if a row contained only one of the player’s mark, and nothing else, then iterate thorough all overlapping rows if an overlapping row contained only one of the player’s mark, and nothing else if it’s not the position in which the two rows overlap, then you’ve found a fork return the position in which the two rows overlap

I already knew how to iterate though all of the rows, but how do you find all of the overlapping rows? It turns out this is easier than I expected. I wrote a method for the Board class called overlapping_rows which takes a row as a parameter.

def overlapping_rows(row)
  self.rows.select{ |overlap| (overlap & row).length > 0 && overlap != row }
end

All this method does is select the rows that contain a position that is also in the row passed in, just as long as it is not the same row. The actual code in the ComputerPlayer class ended up looking like this:

def find_winning_fork_move(board)
  board.rows.each do |row|
    if board.only_one_in_a_row?(row, self.mark)
      overlaps = board.overlapping_rows(row)
      overlaps.each do |overlap|
        if board.only_one_in_a_row?(overlap, self.mark)
          overlapping_move = (overlap & row).first
          return overlapping_move if board.valid?(overlapping_move)
        end
      end
    end
  end
  nil
end

The method returns the position to create a fork as soon as it finds the first fork.

Blocking All Forks, Not Just One

At first, I thought that after I had implemented a method that created forks, I could use the same code to block forks. I figured out there was a problem when I was testing with the following game:

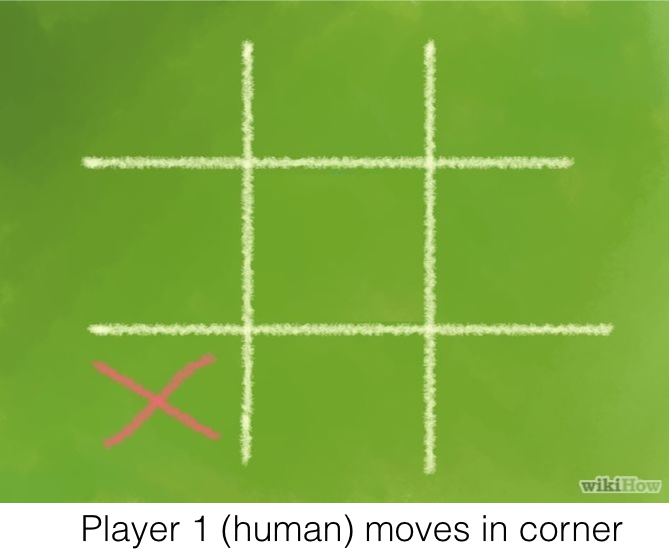
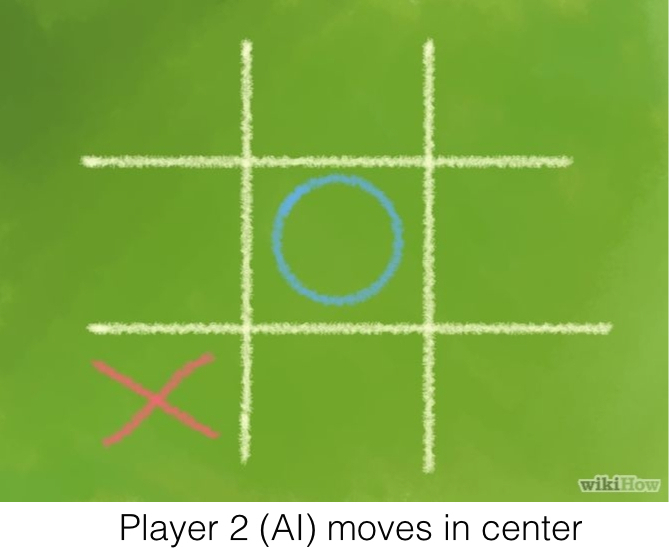
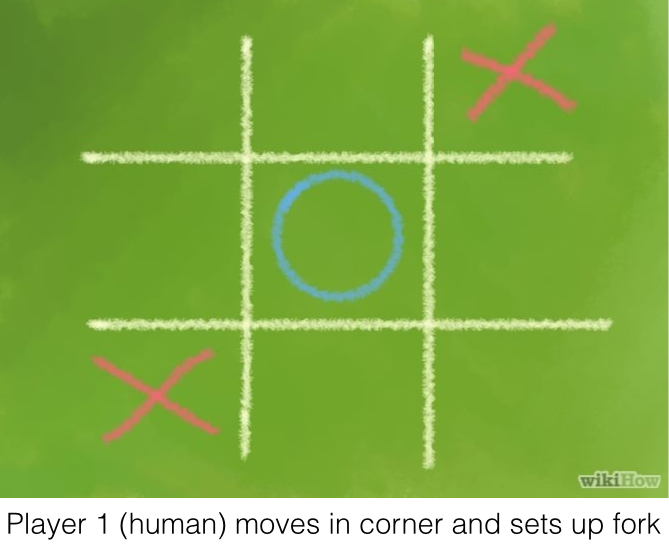
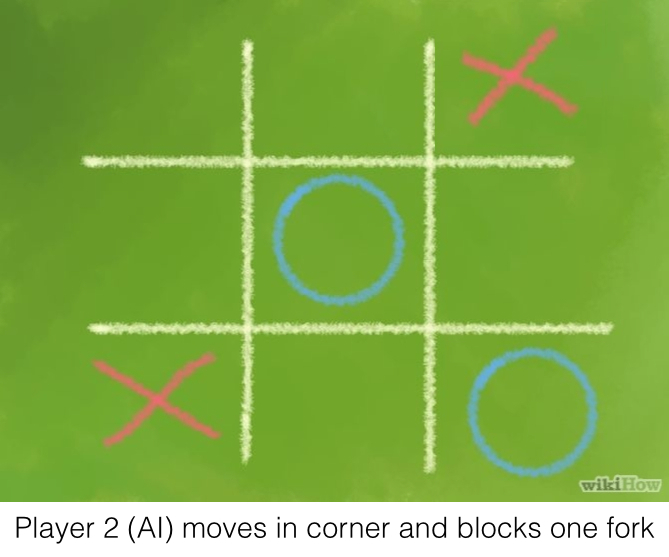
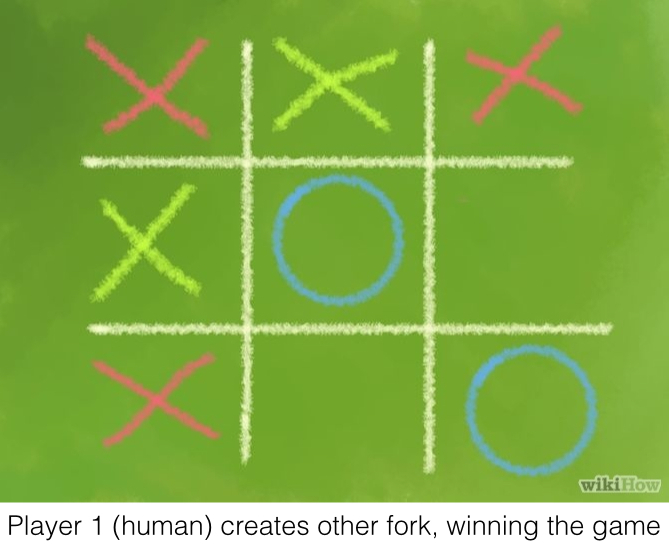
In the process of blocking one fork, the AI had left another one open. Therefore, it wasn’t just as simple as finding the first fork. The AI had to find them all, and then choose the optimal place to block. First, finding all forks:

def find_possible_forks(board, mark)
  possible_forks = []
  board.rows.each do |row|
    if board.only_one_in_a_row?(row, self.opponent_mark)
      overlaps = board.overlapping_rows(row)
      overlaps.each do |overlap|
        if board.only_one_in_a_row?(overlap, self.opponent_mark)
          overlapping_move = (overlap & row).first
          if board.valid?(overlapping_move)
            possible_forks << [row, overlap]
          end
        end
      end
    end
  end
  possible_forks.each{ |fork| fork.sort! }.uniq
end

The only problem with this method is that as it iterates over all rows, it inserts duplicate forks in a different order. Thus, the last line of the method removes these duplicates.

Then, I had to figure out a way to pick the proper blocking spot. I tried things like finding the position that occurs the most in the rows, but it turns out there was no correlation. I finally realized that the way to find the proper blocking move is to look ahead, by checking all moves that would block a fork. I did this in a method called select_blocking_fork_move, which takes a list of possible forks as a parameter. The line

possible_moves = possible_forks.flatten.uniq.select{ |index| board.valid?(index) }

creates an array of possible moves by selecting all position on the board that are open and are on the forking rows.

Then, while iterating over all possible moves, the AI had to look ahead. The possible move is placed on a copy of the board

possible_moves.each do |move|
  test_board = Marshal.load(Marshal.dump(board))
  test_board.set(move, self.mark)
  ...
end

and then, the AI checks for one of two scenarios. First, it checks that if the blocking move creates two in a row, and then the opponent moves to block, it doesn’t create another fork for the opponent. That’s a lot, but I think it makes more sense if you look at the code:

opponent_move = find_winning_move(test_board)
if opponent_move
  test_board.set(opponent_move, self.opponent_mark)
  if !contains_fork?(test_board, self.opponent_mark)
    return move
  end
else
  ...
end
...

As you see, I wrote a method called contains_fork? which checks the board for forks. The else statement within the loop checks if the possible move does, in fact, block all possible forks:

opponent_move = find_winning_move(test_board)
if opponent_move
  test_board.set(opponent_move, self.opponent_mark)
  ...
else
  test_board.set(opponent_move, (opponent_move + 1).to_s)
  if find_possible_forks(test_board, self.opponent_mark).length == 0
    return move
  end
end

The body of the else statement first removes the test opponent mark that had been put on the board, and then checks if there are any possible forks. If there aren’t, even though this move doesn’t create two in a row, it blocks the opponent from creating a fork.

And then, putting it all together:

def select_blocking_fork_move(board, possible_forks)
  possible_moves = possible_forks.flatten.uniq.select{ |index| board.valid?(index) }
  possible_moves.each do |move|
    test_board = Marshal.load(Marshal.dump(board))
    test_board.set(move, self.mark)
    opponent_move = find_winning_move(test_board)
    if opponent_move
      test_board.set(opponent_move, self.opponent_mark)
      if !contains_fork?(test_board, self.opponent_mark)
        return move
      end
    else
      test_board.set(opponent_move, (opponent_move + 1).to_s)
      if find_possible_forks(test_board, self.opponent_mark).length == 0
        return move
      end
    end
  end
  nil
end

Pitfalls

Of course, there are some things that I’m not happy about in terms of how my code turned out.

Breaking from loops using return statements For this project, I am a big offender of breaking out of loops using a return statement. For example, from my ComputerPlayer class:

def find_two_in_a_row(board, mark)
  board.rows.each do |row|
    if board.only_two_in_a_row?(row, mark)
      return board.get_open_position(row)
    end
  end
  nil
end

It’s not very Ruby-like, I know. Because of my C++ and Java background, in which it’s totally kosher to do that, it is one of my first instincts. I did try to refactor and figure out another way, but I think the way I have it now is the most clear, at least to me.

Command-line interface I find it to be a little annoying to use. I guess I could refactor it to be a web application, but that’s a lot more work, and the point of this was to create an unbeatable AI.
Storing rows in Board class The “row” is the only part of this application that’s not object-oriented, which I’m not happy about. In my case, a row is an array of length three that holds three positions on the board. I hardcoded these values and stored them as part of the board. I also dislike how the method overlapping_rows takes a row as an argument, which is just an array. It’s just not right.

In the future, I would figure out how to make a row an object and not just data.

Check Out My Code

Now you know how to solve Tic-Tac-Toe! Yay!

If you want to try to find possible flaws in my logic, or look more at my implementation of Tic-Tac-Toe, please check out the heuristic-solution branch on my Github repository. Or, if you know of a better way to solve this, let me know.