Solving Tic-Tac-Toe, Part II: A Better Way

You may recall that just a couple of days ago I posted a solution on how to solve Tic-Tac-Toe. As it turns out, I greatly overcomplicated the problem. Or, well, kind of. I actually just solved Tic-Tac-Toe for humans. I wrote an algorithm on how humans might go about solving the problem. However, the great thing about computers is that they are not humans. They can do a lot of computations and remember a lot of stuff. There’s an algorithm to solve this problem, and it’s called Minimax.

Minimax

As my Google searches evolved from “tic tac toe strategy” (which had lead me to solving the problem for humans) to “tic tac toe algorithm”, I noticed people talking about this thing called “minimax” on programming forums. I think it’s actually the de facto way to solve Tic-Tac-Toe, as there are hundreds resources which detail how to apply Minimax to Tic-Tac-Toe. Well, oops. I like solving things and I don’t like doing something just because the Internet tells me it’s the right thing to do. In order for me to use it, I had to understand how it works.

Minimax is a decision rule which minimizes the maximum possible loss. It involves one maximizing player (in this case, the AI), and one minimizing player (the human opponent). It was developed for zero-sum game theory, which is the mathematical representation of a situation in which a player’s gain or loss is exactly balanced by the loss or gain of the opponent player. If the total gains of all players are added and total losses of all players are subtracted, the result will be zero, thus zero-sum. There’s also a Minimax theorem, first published by John von Neumann (of von Neumann architecture, which almost all modern computers use) in 1928:

The minimax theorem states:
For every two-person, zero-sum game with finitely many strategies, there exists a value V and a mixed strategy for each player, such that
(a) Given player 2’s strategy, the best payoff possible for player 1 is V, and
(b) Given player 1’s strategy, the best payoff possible for player 2 is −V.

Therefore, the AI needs to pick the move with the best possible payoff. What do all of the moves look like? How do we calculate the payoff?

The Set of Moves Forms a Tree

In Minimax, each possible move is evaluated, given a score, and then compared to the other possible moves. The one with the best payoff is chosen. We have a set of possible moves, which is like a set of paths, and ends up looking something like this:

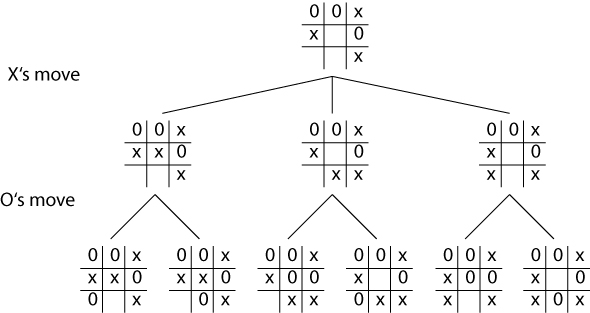
Minimax looks ahead at all possible paths, by scoring the state of the board at its maximum depth, recursively scoring the board in the parent node by choosing the best child, until the score and position reaches the root.

Let’s look at the pseudocode:

def minimax(depth, player)
  if gameover || depth == 0
    return calculated_score
  end
  children = all legal moves for player
  if player is AI (maximizing player)
    best_score = -infinity
    for each child
      score = minimax(depth - 1, opponent)
      if (score > best_score)
        best_score = score
      end
      return best_score
    end
  else #player is minimizing player
    best_score = +infinity
    for each child
      score = minimax(depth - 1, player)
      if (score < best_score)
        best_score = score
      end
      return best_score
    end
  end
end

#then you would call it like
minimax(2, computer)

One important thing to note is the depth. You don’t necessarily need to look ahead at all possible paths, just a few moves ahead. Also notice that this algorithm is recursive and depth-first.

Calculating A Score

How do we actually give a score to the state of of the board? This is the only part of the algorithm that ends up being heuristic. You have to choose a heuristic board evaluation function to calculate this value. I chose to calculate a score for each line (the three rows, the three columns, and two diagonals) on the board, and then sum these values. I scored each line as follows:

+100 for each three-in-a-row for the AI
+10 for each two-in-a-row (and empty cell) for the AI
+1 for each one-in-a-row (and two empty cells) for the AI
-1 for each one-in-a-row (and two empty cells) for the other player
-10 for each two-in-a-row (and empty cell) for the other player
-100 for each three-in-a-row for the other player
0 for all other states

It’s nice how simple it ends up being to score a board state.

Minimax, But Better

There’s a different algorithm that makes Minimax better, called Alpha-beta pruning. This eliminates paths that are worse than paths that have already been evaluated. Therefore, you have to store a few more values: alpha, which holds the maxmimum score for the maximum path, and beta, which holds the minimum score for the minimum path. You throw away a path when its alpha value is >= the beta value. The algorithm is extremely similar, and the pseudo code is as follows:

def minimax(depth, player, alpha, beta)
  if gameover || depth == 0
    return calculated_score
  end
  children = all legal moves for player
  if player is AI (maximizing player)
    for each child
      score = minimax(depth - 1, opponent, alpha, beta)
      if (score > alpha)
        alpha = score
      end
      if alpha >= beta
        break
      end
      return alpha
    end
  else #player is minimizing player
    best_score = +infinity
    for each child
      score = minimax(depth - 1, player, alpha, beta)
      if (score < beta)
        beta = score
      end
      if alpha >= beta
        break
      end
      return beta
    end
  end
end

#then you would call it like
minimax(2, computer, -inf, +inf)

In alpha-beta pruning, the alpha and beta values are passed along with each recursive call of minimax. The path is discarded (by calling break within the loop) if at any moment in the path, alpha is greater than or equal to beta.

The score depends on which player minimax is currently being called on: if it’s the maximizing player (the AI), alpha is returned as the score, and beta if it is the minimizing player.

Check Out My Code

If you would like to see how I implemented alpha-beta pruning for a Tic-Tac-Toe AI, check out my Github repository. The other solution is now on a branch called heuristic-solution.

Also, it’s remarkable how much simpler this solution is versus the heuristic solution. Game theory and decision theory are really cool, and are definitely something I should read about more.

Resources

[1] Minimax at Wikipedia
[2] Alpha-beta pruning at Wikipedia
[3] Zero-sum game at Wikipedia

Ear to the Bits

Ramblings about code